2.3 Span and Linear Independence

1Reading¶

Material related to this page, as well as additional exercises, can be found in ALA Ch. 2.3 and LAA 4.1, 4.3.

2Learning Objectives¶

By the end of this page, you should know:

how to form linear combinations of vectors
a span of a set of vectors
what it means for a collection of vectors to be linearly dependent and independent
how to check for linear dependence and independence

3Span and Linear Independence¶

3.1Building Subspaces¶

One natural way of constructing a subspace is to start with some building blocks $\vv v_1, \dots, \vv v_k\in V$ from the vector space $V$ we are working in, and to consider all possible linear combinations of them.

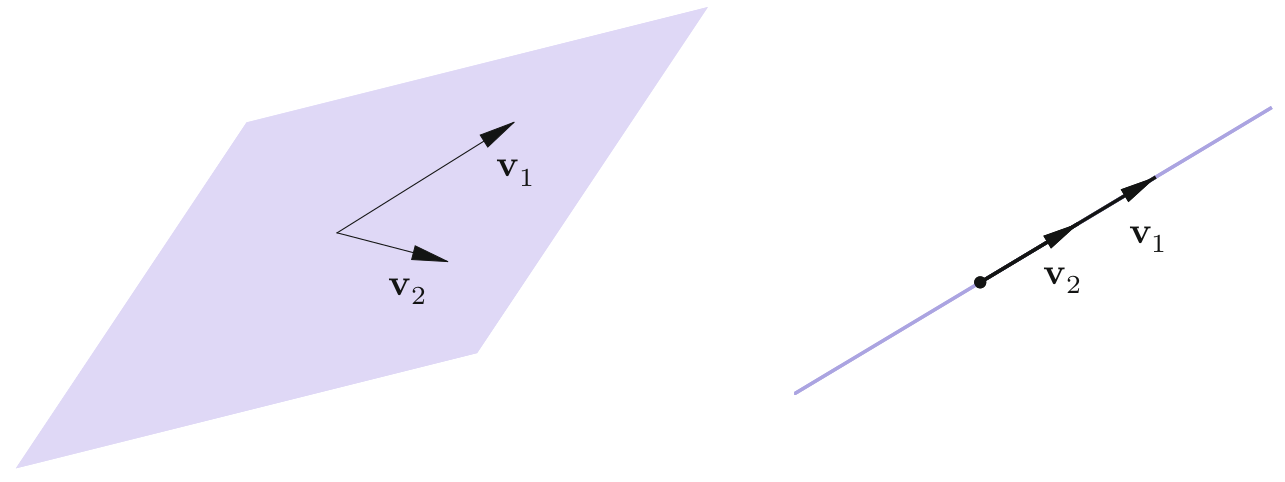
A plane and a line spanned by two vectors $\vv v_1, \vv v_2$ is given in Figure 1. In the case of the line, there is some scalar $c \in \mathbb{R}$ such that $\vv v_1 = c \vv v_2$ .

This key fact is not hard to check using the properties of vector addition and scalar multiplication, but it is a surprisingly powerful tool for generating useful subspaces, and for checking if a vector $\vv v \in V$ also lives in a subspace $W$ .

Exercise 1 (Checking Membership of a Vector in a Span of Vectors)

Let $W = \textrm{span}\{\vv v_1, \vv v_2\} \subset \mathbb{R}^3$ , where

\vv v_1 = \bm 1 \\ 2 \\ 1 \em, \ \vv v_2 = \bm -2 \\ -3 \\ 5 \em.

(3)

Is the vector $\vv v = \bm 1 \\ 3 \\ 8 \em$ an element of $W$ ? How about the vector $\vv{\tilde v} = \bm 1\\0\\0 \em$ ?

Solution to Exercise 1

If $\vv v \in W$ then we can find scalars $c_1, c_2 \in \mathbb R$ such that $\vv v = c_1 \vv{v_1} + c_1 \vv{v_2}$ , that is:

\begin{align*} \bm 0&1&-1 \em = c_1 \bm 1\\-2\\1 \em + c_2\bm 2\\-3\\1\em = \bm c_1 + 2c_2\\-2c_1 - 3c_2\\c_1+c_2 \em \end{align*}

(4)

That is, $c_1$ and $c_2$ must satisfy the linear system:

\begin{align*} c_1 + 2c_2 &= 0\\ -2c_1 - 3c_2 &= 1\\ c_1 + c_2 &= -1 \end{align*}

(5)

which we solve using Gaussian Elimination to get $c_1 = -2, c_2 = 1$ , so that $\vv v = -2 \vv{v_1} + \vv{v_2} \in W$ . On the other hand, $\vv{\tilde v} = \bm 1\\0\\0 \em$ is not in $W$ : setting up a similar system of equations, we would find it has no solution and hence $\vv{\tilde v} \not\in W$ .

3.2Linear Independence and Dependence¶

Linear dependence captures a notion of “redundancy” in a collection of vectors.

The condition (7) implies that we can write at least one of the $\vv v_i$ as a linear combination of the other vectors: hence, it does not add anything new to the span of the collection $\vv v_1 , \ldots , \vv v_k$ .

Example 6

The polynomials $p_1(x) = x - 2$ , $p_2(x) = x^2 - 5x + 4$ , $p_3(x) = 3x^2 - 4x$ , $p_4(x) = x^2 - 1$ are linearly dependent since:

\begin{align*} p_1(x) + p_2(x) - p_3(x) + 2p_4(x) = 0 \quad\text{for all $x$} \end{align*}

(13)

On the other hand, the three polynomials $p_1(x), p_2(x), p_3(x)$ are linearly independent. To see why, suppose

\begin{align*} c_1p_1(x) + c_2p_2(c) + c_3p_3(x) = (c_2 + 3c_3)x^2 + (c_1 - 5c_2 + 4c_3)x - 2c_1 + 4c_2 = 0 \quad\text{for all $x$} \end{align*}

(14)

This is true if $c_2 + 3c_3 = 0, c_1 - 5c_2 - 4c_3 = 0, -2c_1 + 4c_2 = 0$ , which only has the trivial solution $c_1 = c_2 = c_3 = 0$ .

4Checking Linear Independence in $\mathbb{R}^n$ ¶

Given the task of checking whether $\vv v_1 , \ldots , \vv v_k \in \mathbb{R}^n$ is linearly dependent, we start by constructing the $n \times k$ matrix $A = \bm \vv v_1 & \ldots & \vv v_k \em$ with columns defined by $\vv v_i$ . Using matrix-vector multiplication, we interpret (7) as

A \vv c = c_1 \vv v_1 + \ldots + c_k \vv v_k, \ \textrm{where} \ \vv c = \bm c_1 \\ c_2 \\ \vdots \\ c_k \em,

(15)

that is, we write any linear combination of the vectors $\vv v_1, \dots, \vv v_k$ weighted by coefficients $c_1, \dots, c_k$ in terms of matrix multiplication. The above equation helps us relate linear algebraic systems with the geometry of the span of vectors.

Theorem 1

Let $\vv v_1 , \ldots , \vv v_k \in \mathbb{R}^n$ and $A = \bm \vv v_1 & \ldots & \vv v_k \em \in \mathbb{R}^{n \times k}$ . Then

The $\vv v_1 , \ldots , \vv v_k \in \mathbb{R}^n$ are linearly dependent if and only if there is a non-zero solution $\vv c = \vv 0$ to the linear system $A \vv c = 0$ .
The vectors are linearly independent if and only if the only solution to the system $A \vv c = 0$ is the trivial one, $\vv c = \vv 0$ .
A vector $\vv b$ lies in the span of $\vv v_1 , \ldots , \vv v_k$ if and only if the linear system $A \vv c = \vv b$ is compatible, i.e., has at least one solution.

Proof 1 (Proof of Theorem 1)

We prove the ﬁrst statement, leaving the other two as exercises for you. The condition that $\vv v_1 , \ldots , \vv v_k$ be linearly dependent is that there exists a nonzero vector

\vv c = \bm c_1 \\ c_2 \\ \vdots \\ c_k \em \neq \vv 0 \ \textrm{such that} \ A \vv c = c_1 \vv v_1 + \ldots + c_k \vv v_k = \vv 0.

(16)

Therefore, linear dependence requires the existence of a nontrivial solution to the linear system $A \vv c = \vv 0$ .

Exercise 2 (Checking Linear Independence in

\mathbb{R}^4

)

Determine if the vectors

\begin{align*} \bm 1\\2\\3\\4\em, \bm 2\\3\\4\\5\em, \bm 4\\1\\0\\-1\em, \bm 4\\2\\2\\2\em \end{align*}

(17)

are linearly independent or linearly dependent.

Solution to Exercise 2

To determine linear dependence, we check for nontrivial solutions to the system

\begin{align*} \bm 1&2&4&4\\2&3&1&2\\3&4&0&2\\4&5&-1&2 \em \vv x = \vv 0 \end{align*}

(18)

The augmented matrix is given by

\begin{align*} \left[ \begin{array}{cccc|c} 1&2&4&4&0\\ 2&3&1&2&0\\ 3&4&0&2&0\\ 4&5&-1&2&0 \end{array}\right] \end{align*}

(19)

Putting the augmented matrix in row echelon form with Gaussian, we get the equivalent system

\begin{align*} \left[ \begin{array}{cccc|c} 1&2&4&4&0\\ 0&-1&-7&-6&0\\ 0&0&2&2&0\\ 0&0&0&0&0 \end{array}\right] \end{align*}

(20)

Let’s use the pivots to eliminate the entries above them as well:

\begin{align*} \left[ \begin{array}{cccc|c} 1&0&0&2&0\\ 0&-1&0&1&0\\ 0&0&2&2&0\\ 0&0&0&0&0 \end{array}\right] \end{align*}

(21)

This is equivalent to the linear system

\begin{align*} x_1 + 2x_4 &= 0\\ -x_2 + x_4 &= 0\\ 2x_3 + 2x_4 &= 0 \end{align*}

(22)

which has the nontrivial solution

\begin{align*} \bm x_1\\x_2\\x_3\\x_4\em = \bm -2\\ 1\\ -1\\ 1 \em \end{align*}

(23)

Therefore the four given vectors are linearly dependent.