4.4 Orthogonal Projections and Orthogonal Subspaces

1Reading¶

Material related to this page, as well as additional exercises, can be found in ALA 4.4.

2Learning Objectives¶

By the end of this page, you should know:

orthogonal projection of vectors
orthogonal subspaces
relationship between dimensions of orthogonal subspaces
orthogonality of the fundamental matrix subspaces and how they relate to a linear system

3Introduction¶

We extend the idea of orthogonality between two vectors to orthogonality between subspaces. Our starting point is the idea of an orthogonal projection of a vector onto a subspace.

4Orthogonal Projection¶

Let $V$ be a (real) inner product space, and $W \subset V$ be a finite dimensional subspace of $V$ . The results we resent are fairly general, but it may be helpful to think of $W$ as a subspace of $V = \mathbb{R}^m$ .

Note from Definition 2 that this means $\vv v$ can be decomposed as the sum of its orthogonal projection $\vv w \in W$ and the perpendicular vector $\vv z \perp W$ that is orthogonal to $W$ , i.e., $\vv v = \vv w + \vv v - \vv w = \vv w + \vv z$ .

When we have access to an orthonormal basis for $W \subset V$ , constructing the orthogonal projection of $\vv v \in V$ onto $W$ becomes quite simple as given below.

Theorem 1

Let $\vv u_1, \vv u _2, \ldots, \vv u_n$ be an orthonormal basis for the subspace $W \subset V$ . Then, the orthogonal projection of $\vv v \in V$ onto $\vv w \in W$ is given by

\vv w = c_1 \vv u_1 + c_2 \vv u_2 + \ldots + c_n \vv u_n \ \textrm{where} \ c_i = \langle \vv v, \vv u_i \rangle, \ i = 1,2,\ldots,n

(1)

Proof 1 (Proof of Theorem 1)

Since $\vv u_1, \vv u_2, \ldots, \vv u_n$ form a basis for $W$ , we must have that $\vv w = c_1 \vv u_1 + c_2 \vv u_2 + \ldots + c_n \vv u_n$ for some $c_1, \ldots, c_n$ .

If $\vv w$ is an orthogonal projection of $\vv v$ onto $W$ , by definition we must have that $\langle \vv v - \vv w, \vv q \rangle = 0$ for any $\vv q \in W$ . So, let’s pick $\vv q = \vv u_i$ :

\begin{align*} 0 = \langle \vv v - \vv w, \vv u_i \rangle &= \langle \vv v - c_1 \vv u_1 + \ldots + c_n \vv u_n, \vv u_i \rangle \\ &= \langle \vv v , u_i \rangle - c_1 \langle \vv u_1, \vv u_i \rangle - c_2 \langle \vv u_2, \vv u_i \rangle - \ldots - c_i \langle \vv u_i, \vv u_i\rangle - \ldots - c_n \langle \vv u_n, \vv u_i\rangle \\ &= \langle \vv v, \vv u_i\rangle - c_i \end{align*}

(2)

where, the last line follows from $\vv u_1, \vv u_2, \ldots \vv u_n$ being an orthonormal basis for $W$ . Repeating for $i=1,2,\ldots,n$ , we conclue that $c_i = \langle \vv v, \vv u_i\rangle$ for $i=1,\ldots,n$ are uniquely prescribed by the orthogonality requirement, satisfying uniqueness.

Example 1

Consider the plane $W \subset \mathbb{R}^3$ spanned by orthogonal (but not orthonormal!) vectors

\vv v_1 = \bm 1 \\ -2 \\ 1\em \ \textrm{and} \ \vv v_2 = \bm 1 \\ 1 \\ 1\em

(3)

Let’s compute the orthogonal projection of $\vv v = \bm 1 \\ 0 \\ 0\em$ onto $W = \textrm{span}(\vv v_1, \vv v_2)$ . First, we normalize $\vv v_1$ and $\vv v_2$ :

\vv u_1 = \frac{\vv v_1}{\|\vv v_1\|} = \frac{1}{\sqrt{6}}\bm 1 \\ -2 \\ 1\em, \ \vv u_2 = \frac{\vv v_2}{\|\vv v_2\|} = \frac{1}{\sqrt{3}}\bm 1 \\ 1 \\ 1\em

(4)

and then compute the projection $\vv w$ as

\begin{align*} \vv w &= \langle \vv v, \vv u_1\rangle \vv u_1 + \langle \vv v, \vv u_2\rangle \vv u_2 \\ &= \frac{1}{6}\bm 1 \\ -2 \\ 1\em + \frac{1}{3}\bm 1 \\ 1 \\ 1\em \\ &= \bm \frac{1}{2} \\ 0 \\ \frac{1}{2} \em \end{align*}

(5)

We will see shortly that orthogonal projections of a vector onto a subspace is exactly what solving a least-squares problem does, and lies at the heart of machine learning and data science.

However, before that, we will explore the idea of orthogonal subspaces, and see that they provide a deep and elegant connection between the four fundamental subspaces of a matrix $A$ and whether a linear system $A \vv x=\vv b$ has a solution.

5Orthogonal Subspaces¶

An important geometric notion present in Example 2 is the Orthogonal Complement that is defined below.

The orthogonal complement to a line is given in the figure below, which is discussed in Example 2.

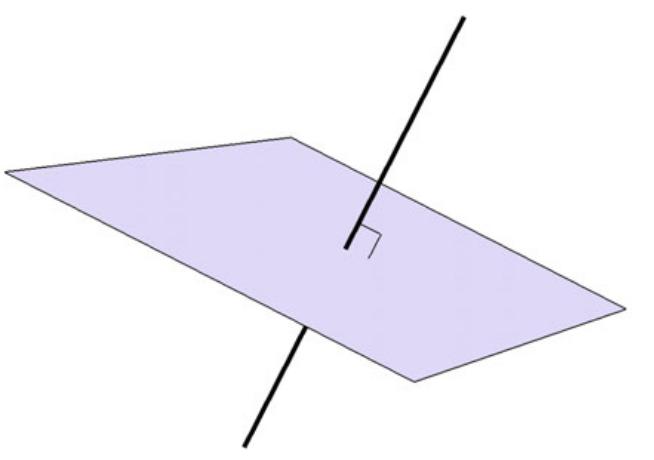
Another direct consequence of Figure 3 is that a subspace and its orthogonal complement have complementary dimensions.

In Example 3, $W \subset \mathbb{R}^3$ is plane, with dim $W = 2$ . Hence, we can conclude that dim $W^{\perp} = 1$ , i.e., $W^{\perp}$ is a line, which is indeed what we saw previously.

Example 4

Let $W = \{ \bm t & -t & 2 t \em^{\top} | t \in \mathbb{R} \}$ be the line (one-dimensional subspace) in the direction of the vector $\vv w_1 = \bm 1 & -1 & 2 \em \in \mathbb{R}^3$ . Let us decompose the vector $\mathbf{v} = \bm 1 & 0 & 1 \em^T \in \mathbb{R}^3$ into a sum $\mathbf{v} = \mathbf{w} + \mathbf{z}$ of a vector $\mathbf{w}$ lying on the line $W$ and a vector $\mathbf{z}$ belonging to its orthogonal plane $W^\perp$ . Each is obtained by an orthogonal projection onto the subspace in question, but we only need to compute one of the two directly, since the second can be obtained by subtracting the first from $\mathbf{v}$ .

Orthogonal projection onto a one-dimensional subspace is easy, since every basis is, trivially, an orthogonal basis. Thus, the projection of $\mathbf{v}$ onto the line spanned by

\mathbf{w}_1 = \bm 1 & -1 & 2 \em^{\top} \quad \text{is} \quad \mathbf{w} = \frac{\langle \mathbf{v}, \mathbf{w}_1 \rangle}{\|\mathbf{w}_1\|^2} \mathbf{w}_1 = \bm\frac{1}{2} & \frac{-1}{2} & 1\em^{\top}.

(7)

The component in $W^\perp$ is then obtained by subtraction:

\mathbf{z} = \mathbf{v} - \mathbf{w} = \bm\frac{1}{2} & \frac{1}{2} & 0\em^{\top}.

(8)

6Orthogonality of the Fundamental Matrix Subspace¶

We previously introduced the four fundamental subspaces associated with an $m \times n$ matrix $A$ : the column, null, row, and left null spaces. We also saw that the null and row spaces are subspaces with complementary dimensions in $\mathbb{R}^n$ , and the left null space and column space are subspaces with complementary dimensions in $\mathbb{R}^m$ . Moreover, these pairs are orthogonal complements of each other with respect to the standard dot product.

We will not go through the proof (although it is not hard), but instead focus on a very important practical consequence.

Theorem 3 (Fredholm Alternative)

A linear system $A \vv x = \vv b$ has a solution if and only if $\vv b$ is orthogonal to LNull $(A)$ .

Proof 2 (Proof of Theorem 3)

We know that $A \vv x = \vv b$ if and only if $b \in$ Col $(A)$ since $A \vv x$ is a linear combination of the columns of $A$ .

From Theorem 2 we know that $\textrm{LNull}(A) = \textrm{Col}(A)^{\perp}$ , or equivalently, that $\textrm{Col}(A) = \textrm{LNull}(A)^{\perp} = \textrm{Null}(A^{\top})^{\perp}$ .

So, this means that $\vv b \in$ Null $(A^{\top})^{\perp}$ , or equivalently, that $\langle \vv y, \vv b\rangle = 0$ for all $\vv y$ such that $A^{\top}\vv y = \vv 0$ . Just to get a sense of why this is perfectly reasonable, let’s assume that we can find a $\vv y \in$ Null $(A)^{\top}$ for which $\langle \vv y, \vv b\rangle \neq 0$ . This implies that we have an inconsistent set of equations, which can be seen as follows.

Let $\vv x$ be any solution to $A \vv x = \vv b$ , and take the inner product of both sides with $\vv y$ :

\langle \vv y, A \vv x\rangle = \langle \vv y, \vv b\rangle.

(10)

But since $\vv y \in$ LNull $(A)$ , $\langle \vv y, A \vv x\rangle = \vv y^{\top} A \vv x = 0$ for any $\vv x$ , meaning we must have $\langle \vv y, \vv b\rangle = 0$ . However, we picked a special $\vv y$ such that $\langle \vv y, \vv b\rangle \neq 0$ . There is a contradiction! This might have been because of a mistake in our reasoning: either $A \vv x = \vv b$ has no solution, or $\langle \vv y, \vv b \rangle = 0$ .

Another way of thinking about (10): if $\vv y^{\top} A \vv x = 0$ , which means we can add the equations in the entries of $A \vv x$ together, weighted by the elements of $\vv y$ , so that they cancel to zero. So, the only way for $A \vv x = \vv b$ to be compatible is if the same weighted combination of the RHS, $\vv y^{\top} \vv b$ , also equals 0.