5.1 Linear Functions a simple function class
Dept. of Electrical and Systems Engineering
University of Pennsylvania
1 Reading ¶ Material related to this page, as well as additional exercises, can be found in ALA 7.1.
2 Learning Objectives ¶ By the end of this page, you should know:
definition of Linear functions and some examples how to verify linearity of functions how matrix-vector multiplication relates to linear functions composition of linear functions inverses of linear functions 3 Introduction to Linearity ¶ A strategy that we have embraced so far has been to turn algebraic questions into geometric ones. Our foundation for this strategy has been the vector space, which allows us to reason abut a wide range of objects (vectors, polynomials, word histograms, and functions) as “arrows” that we can add, stretch, flip and rotate. Our canonical approach to transforming one vector into another has been through matrix-vector multiplication: we start with a vector x \vv x x x ↦ A x \vv x \mapsto A \vv x x ↦ A x
Our goal in this lecture is to give you a brief introduction to the theory of linear functions , of which the function
f ( x ) = A x f(\vv x) =A \vv x f ( x ) = A x
4 Linear Functions ¶ We start with the basic definition of a linear function which captures the fundamental idea of linearity: closed under addition and scalar multiplication. A formal definition is given below.
Definition 1 (Linear Function)
Let V V V W W W L : V → W L:V \to W L : V → W domain V V V to the codomain W W W is called linear if it obeys two basic rules:
L ( v + w ) = L ( v ) + L ( w ) (L1) L ( c v ) = c L ( v ) (L2) \begin{align*}
L(\vv v+ \vv w) &= L(\vv v) + L(\vv w) \ &\text{(L1)} \\
L(c\vv v) &= cL(\vv v) \ &\text{(L2)}
\end{align*} L ( v + w ) L ( c v ) = L ( v ) + L ( w ) = c L ( v ) (L1) (L2) for all v , w ∈ V \vv v,\vv w \in V v , w ∈ V c ∈ R c \in \mathbb{R} c ∈ R
Before looking at some common examples, we make a few comments:
Setting c = 0 c = 0 c = 0 rule (L2) 0 ∈ V \vv 0 \in V 0 ∈ V 0 ∈ W \vv 0 \in W 0 ∈ W note: these are different zero elements as they live in different vector spaces! ). A commonly used trick for verifying linearity is to combine (L1) (L2) L ( c v + d w ) = c L ( v ) + d L ( w ) for all v , w ∈ V , c , d ∈ R (L) L(c\vv v + d\vv w) = cL(\vv v) + dL(\vv w)\quad \text{for all} \quad \vv v, \vv w \in V, \quad c,d \in \mathbb{R} \quad \text{(L)} L ( c v + d w ) = c L ( v ) + d L ( w ) for all v , w ∈ V , c , d ∈ R (L) We can extend rule (L) L ( c 1 v 1 + ⋯ + c k v k ) = c 1 L ( v 1 ) + ⋯ + c k L ( v k ) (LL) L(c_1\vv v_1 + \cdots + c_k\vv v_k) = c_1L(\vv v_1) + \cdots + c_kL(\vv v_k) \quad \text{(LL)} L ( c 1 v 1 + ⋯ + c k v k ) = c 1 L ( v 1 ) + ⋯ + c k L ( v k ) (LL) for all c 1 , … , c k ∈ R c_1,\ldots,c_k \in \mathbb{R} c 1 , … , c k ∈ R v 1 , … , v k ∈ V \vv v_1,\ldots,\vv v_k \in V v 1 , … , v k ∈ V
Finally a quick note on terminology: we will use linear function and linear map interchangeably when V V V W W W linear transformation when V = W V = W V = W linear operator when V V V W W W
Example 1 (Zero, Identity, and Scalar Multiplication Functions)
The zero function O ( v ) = 0 O(\vv v) = \vv 0 O ( v ) = 0 v ∈ V \vv v \in V v ∈ V 0 ∈ W \vv 0 \in W 0 ∈ W rule (L) The identity function I ( v ) = v I(\vv v) = \vv v I ( v ) = v v ∈ V \vv v \in V v ∈ V rule (L) I ( c v + d w ) = c v + d w I(c\vv v + d\vv w) = c\vv v + d\vv w I ( c v + d w ) = c v + d w c I ( v ) + d I ( w ) = c v + d w cI(\vv v) + dI(\vv w) = c\vv v + d\vv w c I ( v ) + d I ( w ) = c v + d w The scalar multiplication function M a ( v ) = a v M_a(\vv v) = a\vv v M a ( v ) = a v v ∈ V \vv v \in V v ∈ V a ∈ R a \in \mathbb{R} a ∈ R V V V M 0 ( v ) = O ( v ) M_0(\vv v) = O(\vv v) M 0 ( v ) = O ( v ) M 1 ( v ) = I ( v ) M_1(\vv v) = I(\vv v) M 1 ( v ) = I ( v ) We made no assumptions about V V V W W W Example 1
Example 2 (Matrix Multiplication)
Let V = R n V = \mathbb{R}^n V = R n W = R m W = \mathbb{R}^m W = R m A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n L ( v ) = A v L(\vv v) = A\vv v L ( v ) = A v
A ( c v + d w ) = c A v + d A w for all v , w ∈ R n and c , d ∈ R
A(c\vv v + d\vv w) = cA\vv v + dA\vv w \ \text{for all} \ \vv v,\vv w \in \mathbb{R}^n \ \text{and} \ c,d \in \mathbb{R} A ( c v + d w ) = c A v + d A w for all v , w ∈ R n and c , d ∈ R by the basic properties of matrix-vector multiplication.
In fact, matrix-vector multiplications are not only a familiar example of linear maps between Eucledian space, they are the only ones !
Pay attention to the order of m m m n n n L : R n → R m L: \mathbb{R}^n \to \mathbb{R}^m L : R n → R m R n \mathbb{R}^n R n R m \mathbb{R}^m R m A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n m m m n n n
Let’s consider the function R θ : R 2 → R 2 R_{\theta}: \mathbb{R}^2 \to \mathbb{R}^2 R θ : R 2 → R 2 v ∈ R 2 {\vv v \in \mathbb{R}^2} v ∈ R 2 figure
Recalling that ∥ e 1 ∥ = ∥ e 2 ∥ = 1 \|\vv e_1\| = \|\vv e_2\| = 1 ∥ e 1 ∥ = ∥ e 2 ∥ = 1
R θ ( e 1 ) = [ cos θ sin θ ] , R θ ( e 2 ) = [ − sin θ cos θ ]
R_{\theta} (\vv e_1) = \begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix}, \quad
R_{\theta} (\vv e_2) = \begin{bmatrix} -\sin \theta \\ \cos \theta \end{bmatrix} R θ ( e 1 ) = [ cos θ sin θ ] , R θ ( e 2 ) = [ − sin θ cos θ ] which, when stacked together, give the matrix representation R θ ( v ) = A θ v R_{\theta} (\vv v) = A_{\theta} \vv v R θ ( v ) = A θ v
A θ = [ cos θ − sin θ sin θ cos θ ] A_{\theta} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} A θ = [ cos θ sin θ − sin θ cos θ ] This looks familiar! Indeed, this orthogonal 2x2 matrices v ↦ A θ v \vv v \mapsto A_{\theta} \vv v v ↦ A θ v
v ^ = R θ ( v ) = A θ v = [ cos θ − sin θ sin θ cos θ ] [ v 1 v 2 ] = [ v 1 cos θ − v 2 sin θ v 1 sin θ + v 2 cos θ ]
\hat{\vv v} = R_{\theta} (\vv v) = A_{\theta} \vv v = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} v_1 \cos \theta - v_2 \sin \theta \\ v_1 \sin \theta + v_2 \cos \theta \end{bmatrix} v ^ = R θ ( v ) = A θ v = [ cos θ sin θ − sin θ cos θ ] [ v 1 v 2 ] = [ v 1 cos θ − v 2 sin θ v 1 sin θ + v 2 cos θ ] which you can check are correct using trigonometry, but follow directly from the linearity of rotation.
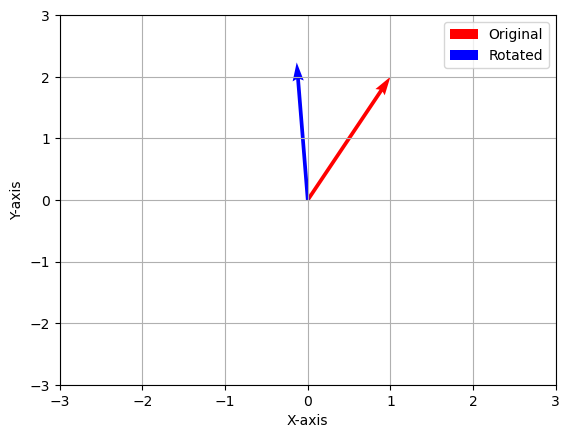
4.1 Python break! ¶ In the below example, we illustrate the rotation of vectors in Python by constructing a rotation matrix as given in Example 3
import numpy as np
import matplotlib.pyplot as plt
def plot_vecs(origin, v1, v2):
fig, ax = plt.subplots()
ax.quiver(*origin, *v1, angles='xy', scale_units='xy', scale=1, color='r', label='Original')
ax.quiver(*origin, *v2, angles='xy', scale_units='xy', scale=1, color='b', label='Rotated')
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
plt.legend()
plt.grid()
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
plt.show()
def rot_mat_cons(theta):
return np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]])
theta = np.pi/6 # change this and observe how much the vector is rotated
rot_mat = rot_mat_cons(theta)
v1 = np.array([[1, 2]]).T
v2 = rot_mat @ v1
# Define the origin
origin = np.array([[0, 0]]).T
plot_vecs(origin, v1, v2)5 Composition ¶ Applying one linear function after another is called composition : let V , W , Z V, W, Z V , W , Z L : V → W L: V \to W L : V → W M : W → Z M: W \to Z M : W → Z composite function M ∘ L : V → Z M \circ L: V \to Z M ∘ L : V → Z ( M ∘ L ) ( v ) = M ( L ( v ) ) (M \circ L)(\vv v) = M(L(\vv v)) ( M ∘ L ) ( v ) = M ( L ( v )) (L)
This gives us a “dynamic” interpretation of matrix-matrix multiplication. If L ( v ) = A v L(\vv v) = A\vv v L ( v ) = A v R n \mathbb{R}^n R n R m \mathbb{R}^m R m M ( w ) = B w M(\vv w) = B\vv w M ( w ) = B w R m \mathbb{R}^m R m R l \mathbb{R}^l R l A ∈ R m × n A \in \mathbb{R}^{m \times n} A ∈ R m × n B ∈ R l × m B \in \mathbb{R}^{l \times m} B ∈ R l × m
( M ∘ L ) ( v ) = M ( L ( v ) ) = B ( A v ) = ( B A ) v
(M \circ L)(\vv v) = M(L(\vv v)) = B(A\vv v) = (BA)\vv v ( M ∘ L ) ( v ) = M ( L ( v )) = B ( A v ) = ( B A ) v so that the matrix representation of M ∘ L : R n → R l M \circ L: \mathbb{R}^n \to \mathbb{R}^l M ∘ L : R n → R l B A ∈ R l × n BA \in \mathbb{R}^{l \times n} B A ∈ R l × n
Example 4 (Composing rotations)
Composing two rotations results in another rotation: R ϕ ∘ R θ = R ϕ + θ R_{\phi} \circ R_{\theta} = R_{\phi + \theta} R ϕ ∘ R θ = R ϕ + θ θ + ϕ \theta + \phi θ + ϕ
[ cos ϕ − sin ϕ sin ϕ cos ϕ ] [ cos θ − sin θ sin θ cos θ ] = A ϕ A θ = A ϕ + θ = [ cos ( ϕ + θ ) − sin ( ϕ + θ ) sin ( ϕ + θ ) cos ( ϕ + θ ) ] \begin{bmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} = A_{\phi} A_{\theta} = A_{\phi+\theta} = \begin{bmatrix} \cos( \phi+\theta) & -\sin(\phi+\theta) \\ \sin(\phi+\theta) & \cos(\phi+\theta) \end{bmatrix} [ cos ϕ sin ϕ − sin ϕ cos ϕ ] [ cos θ sin θ − sin θ cos θ ] = A ϕ A θ = A ϕ + θ = [ cos ( ϕ + θ ) sin ( ϕ + θ ) − sin ( ϕ + θ ) cos ( ϕ + θ ) ] Working out the LHS above, we can derive the well-known trigonometric addition formulas:
c o s ( ϕ + θ ) = cos ϕ cos θ − sin ϕ sin θ , sin ( ϕ + θ ) = cos ϕ sin θ + sin ϕ cos θ cos(\phi+\theta) = \cos \phi \cos \theta- \sin \phi \sin \theta, \quad \sin(\phi+\theta) = \cos \phi \sin \theta + \sin \phi \cos \theta cos ( ϕ + θ ) = cos ϕ cos θ − sin ϕ sin θ , sin ( ϕ + θ ) = cos ϕ sin θ + sin ϕ cos θ In fact, this counts as a proof!
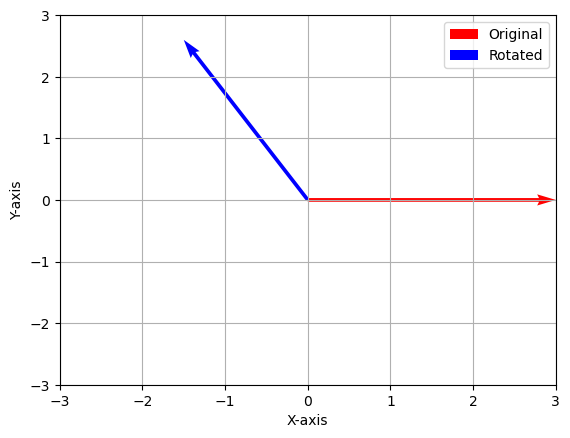
5.1 Python break! ¶ In the below code, we illustrate composition of rotations in Python by multiplying rotation matrices.
theta1 = np.pi/6
theta2 = np.pi/2
rot1 = rot_mat_cons(theta1)
rot2 = rot_mat_cons(theta2)
v1 = np.array([[3, 0]]).T
v2 = rot1 @ rot2 @ v1 # composition of rotations
plot_vecs(origin, v1, v2)
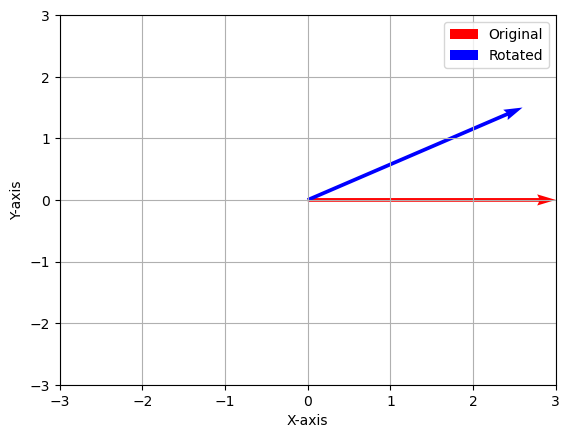
## A reverse rotation
theta3 = -np.pi/2
rot3 = rot_mat_cons(theta3)
v3 = rot3 @ rot1 @ rot2 @ v1 # How can you get to v3 from v2?
plot_vecs(origin, v1, v3)6 Inverses ¶ Just as with square matrices, we can define the inverse of a linear function. Let L : V → W L: V \to W L : V → W M : W → V M: W \to V M : W → V linear function such that:
L ∘ M = I W and M ∘ L = I V L \circ M = I_W \quad \text{and} \quad M \circ L = I_V L ∘ M = I W and M ∘ L = I V where I W I_W I W I V I_V I V W W W V V V M M M inverse of L L L and is denoted M = L − 1 M = L^{-1} M = L − 1
Example 5 (Mapping polyamials
P ( n ) P^{(n)} P ( n ) to
R n \mathbb{R}^n R n and back again)
Let V = P ( n ) V = P^{(n)} V = P ( n ) ≤ n \leq n ≤ n W = R n + 1 W = \mathbb{R}^{n+1} W = R n + 1 L : P ( n ) → R n + 1 L : P^{(n)} → \mathbb{R}^{n+1} L : P ( n ) → R n + 1 p ( x ) = a 0 + a 1 x + ⋯ + a n x n p(x) = a_0 + a_1x + \cdots + a_nx^n p ( x ) = a 0 + a 1 x + ⋯ + a n x n
L ( p ) = [ a 0 a 1 ⋮ a n ] ,
L(p) =\bm
a_0 \\ a_1 \\ \vdots \\ a_n
\em, L ( p ) = ⎣ ⎡ a 0 a 1 ⋮ a n ⎦ ⎤ , i.e, L ( p ) L(p) L ( p ) p ( x ) p(x) p ( x ) L ( p ) ∈ R n + 1 L(p) \in \mathbb{R}^{n+1} L ( p ) ∈ R n + 1
The inverse map L − 1 ( a ) L^{-1}(\vv a) L − 1 ( a ) a = [ a 0 , a 1 , … , a n ] ⊤ ∈ R n + 1 \vv a = \bm a_0 ,a_1, \ldots, a_n\em^{\top} \in \mathbb{R}^{n+1} a = [ a 0 , a 1 , … , a n ] ⊤ ∈ R n + 1 L − 1 ( a ) ( x ) = a 0 + a 1 x + ⋯ + a n x n L^{−1}(\vv a)(x) = a_0 + a_1x + \cdots + a_nx^n L − 1 ( a ) ( x ) = a 0 + a 1 x + ⋯ + a n x n
L ∘ L − 1 = I R n + 1 and L − 1 ∘ L = I p ( n )
L \circ L^{−1} = I_{\mathbb{R}^{n+1}} \ \text{and} \ L^{−1} \circ L = I_{p^{(n)}} L ∘ L − 1 = I R n + 1 and L − 1 ∘ L = I p ( n ) First,
( L ∘ L − 1 ) ( a ) = L ( L − 1 ( a ) ) = L ( ( a 0 + a 1 x + ⋯ + a n x n ) = [ a 0 a 1 ⋮ a n ] = a (L \circ L^{−1})(\vv a) = L (L^{−1}(\vv a)) = L((a_0 + a_1x + \cdots + a_nx^n) = \bm
a_0\\ a1\\ \vdots \\ a_n \em = \vv a ( L ∘ L − 1 ) ( a ) = L ( L − 1 ( a )) = L (( a 0 + a 1 x + ⋯ + a n x n ) = ⎣ ⎡ a 0 a 1 ⋮ a n ⎦ ⎤ = a for any a ∈ R n + 1 \vv a \in \mathbb{R}^{n+1} a ∈ R n + 1 L ∘ L − 1 = I R n + 1 L \circ L^{−1} = I_{\mathbb{R}^{n+1}} L ∘ L − 1 = I R n + 1 p ( x ) = a 0 + a 1 x + ⋯ + a n x n p(x) =
a_0 + a_1x+ \cdots + a_nx^n p ( x ) = a 0 + a 1 x + ⋯ + a n x n
( L − 1 ∘ L ) ( p ) = L − 1 ( L ( p ) ) = L − 1 ( [ a 0 a 1 ⋮ a n ] ) = L − 1 ( a ) = a 0 + a 1 × + ⋯ + a n x n = p ( x )
(L^{−1} \circ L) (p) = L^{−1}(L(p)) = L^{−1}\left(\bm
a_0 \\ a_1 \\ \vdots \\
a_n \em \right) = L^{−1}(\vv a) = a_0+a_1×+ \cdots +a_nx^n = p(x) ( L − 1 ∘ L ) ( p ) = L − 1 ( L ( p )) = L − 1 ⎝ ⎛ ⎣ ⎡ a 0 a 1 ⋮ a n ⎦ ⎤ ⎠ ⎞ = L − 1 ( a ) = a 0 + a 1 × + ⋯ + a n x n = p ( x ) So that L − 1 ∘ L = I p ( n ) L^{−1}\circ L = I_{p(n)} L − 1 ∘ L = I p ( n )
Because there exists an invertible linear map between R n + 1 \mathbb{R}^{n+1} R n + 1 P ( n ) P^{(n)} P ( n ) isomorphic . As we saw earlier in the semester, this means that “they behave the same” and we can do vector space operations in either R n + 1 \mathbb{R}^{n+1} R n + 1 P ( n ) P^{(n)} P ( n )
A more general statement can be made than the previous one: any vector space of dimension n n n R n \mathbb{R}^n R n all finite dimensional vector spaces .