3.4 Distance and Nearest Neighbors

1Reading¶

Material related to this page, as well as additional exercises, can be found in VMLS 3.2.

2Learning Objectives¶

By the end of this page, you should know:

the Euclidean distance between two vectors
the properties of a general distance function

3The Euclidean Distance¶

A distance function, or metric, describes how far apart 2 points are.

A familiar starting point for our study of distances will be the Euclidean distance, which is closely related to the Euclidean norm on $\mathbb R^n$ :

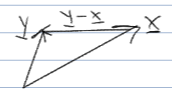
Note that this is measuring the length of the arrow drawn from point $\vv x$ to point $\vv y$ :

Euclidean distance bewteen 2 vectors $\vv x$ and $\vv y$

3.1Python break!¶

We use the np.linalg.norm function in Python to compute the Eucledian distance between two vectors by computing the norm of the difference between the vectors.

# Distance between vectors
import numpy as np

v1 = np.array([1, 2])
v2 = np.array([3, 4])
euc_dist = np.linalg.norm(v1 - v2)
print("Eucledian distance: ", euc_dist)

Eucledian distance:  2.8284271247461903

4General Distances¶

In this course, we will only work with the Euclidean distance. However, given any vector space with a general norm (i.e., $\mathbb{R}^n$ with the Euclidean norm), we may construct a distance function as the norm of their difference. This leads us to a more general notion of distances:

Try to convince yourself why the Euclidean distance fits this definition.

When the distance $\| \vv x - \vv y \|$ between two vectors $\vv x, \vv y \in V$ is small, we say they are “close.” If the distance between $\| \vv x - \vv y \|$ is large, we say they are “far.” What constitutes close or far is typically application dependent.

Note that one vector space can admit many distance functions. From here on, unless otherwise mentioned, we will only be considering the Euclidean distance.

Example 1 (Matrix Norms and their Induced Distances)

Let $M \in \mathbb{R}^{n \times n}$ be a symmetric square matrix such that $x^T M x > 0$ for all nonzero $x\in \mathbb{R}^n$ . Such a matrix is called positive definite; some equivalent definitions of positive definite matrices are symmetric matrices which may be decomposed as $A^TA$ , where $A$ is an invertible square matrix, or symmetric matrices with all strictly positive eigenvalues. A familiar positive definite matrix is the identity matrix, $I_n$ .

Then, $M$ induces an inner product given by $\langle \vv u, \vv v \rangle_M = \vv u^T M \vv v$ . In the case that $M$ is diagonal, this is the weighted dot product we have seen before. Try for yourselves to verify that $\langle \vv u, \vv v \rangle_M$ indeed satisfies all axioms of an inner product.

The inner product in turn induces a norm $\|\vv v\|_M = \sqrt{\langle \vv v, \vv v\rangle}_M = \sqrt{\vv v^T M \vv v}$ .

TODO: Probably want to move this to the norms lesson

Example 2 (Distances on a Connected Graph)

In this example, we’ll demonstrate how the definition of a distance function can be satisfied when the underlying space isn’t a vector space. We will consider the shortest walk distance on a connected undirected graph.

An undirected graph consists of a set of vertices and edges which connect 2 vertices. Often times, undirected graphs are drawn as follows: the vertices are dots, and edges are lines connecting 2 dots. So we can represent an example of an undirected graph with the image below. (For our purposes, we will assume that each pair of vertices can have at most 1 edge connecting them, and that no vertex has an edge to itself.)

A walk in an undirected graph is a sequence of vertices $v_1, v_2, ..., v_{k - 1}, v_k$ such that there is an edge between adjacent vertices in this sequence. The number of edges in the walk is its length. In the image, for example, $3 \to 5\to 6\to 10$ is a walk with length 3.

We say an undirected graph is connected if there is at least one walk between every pair of vertices. The above graph is connected.

If a graph is connected, then we can define the shortest walk distance as follows. For vertices $u, v$ in our graph, their shortest walk distance is defined as

\begin{align*} \text{dist}(u, v) = \text{length of shortest walk starting at $u$ and ending at $v$} \end{align*}

(6)

We will verify that the shortest walk distance indeed satisfies the three axioms of a distance function.

Symmetry. For any two vertices $u, v$ , let $P = u \to ... \to v$ be a minimum length walk (with length $l$ ) starting at $u$ and ending at $v$ . If we reverse $P$ , we get a walk starting at $v$ and ending at $u$ with length $l$ . This means that $d(v, u) \leq l = d(u, v)$ .
Next, let $Q = v\to ...\to u$ be a minimum length walk starting at $v$ and ending at $u$ (with length $l'$ ). If we reverse $Q$ , we get a walk starting at $u$ and ending at $v$ with length $l'$ . This means that $d(u, v) \leq l' = d(v, u)$ .
Taken together, these two inequalities imply that $d(u, v) = d(v, u)$ , i.e., the shortest walk distance is symmetric.
Positivity. For vertices $u \neq v$ , it will take at least one edge to go from $u$ to $v$ , implying that $d(u, v) > 0$ if $u \neq v$ . Also, $d(v, v) = 0$ because we can take the trivial walk $P = v$ , which has no edges.
Triangular Inequality. For vertices $u, v, w$ , we want to show that
$\begin{align*} d(u, w) \leq d(u, v) + d(v, w) \end{align*}$
(7)
Note that if $P_{uv}$ is a walk of length $d(u, v)$ from $u$ to $v$ , and $P_{vw}$ is a walk of length $d(v, w)$ from $v$ to $w$ , then we can concatenate $P_{uv} \to P_{vw}$ to get a walk starting from $u$ which ends at $w$ and has length $d(u, v) + d(v, w)$ . Since the shortest walk from $u$ to $w$ can’t be longer than this walk we just constructed, this implies that $d(u, w) \leq d(u, v) + d(v, w)$ , i.e., the triangular inequality holds.

5Applications of Distances¶

Example 4 (Nearest Neighbors)

Suppose we are given a collection $\vv {z_1}, ..., \vv {z_m} \in V$ of $m$ vectors living in a vector space $V$ . We say that $\vv{z_j}$ is the nearest neighbor of $\vv {x}$ among the vectors $\vv {z_1}, ..., \vv {z_m} \in V$ if

\begin{align*} \| \vv x - \vv{z_j} \| \leq \| \vv x - \vv{z_i} \| \quad\text{for i = 1, ..., m} \end{align*}

(8)

In words, this means $\vv{z_j}$ is the closest vector to $\vv x$ among $\vv{z_1}, ..., \vv{z_m}$ . This is illustrated below; we note that the nearest neighbor may not be unique (e.g., if several $\vv{z_i}$ satisfy the condition above).

$Nearest neighbor to a vector $\vv x \in \mathbb{R}^2$$