6.8 Linear Ordinary Differential Equations

1Reading¶

Material related to this page, as well as additional exercises, can be found in ALA 8.1.

2Learning Objectives¶

By the end of this page, you should know:

how to recognize linear dynamical systems,
how to find the solution to a linear ordinary differential equation.

3Linear Dynamical Systems¶

A dynamical system refers to the differential equations governing the change of a system over time. This system can be mechanical, electrical, fluid, biological, financial, or even social. In this page, we will learn how to solve special differential equations describing linear dynamical systems. We will draw heavily on the concepts of eigenvalues and eigenvectors covered in the previous pages.

3.1Scalar Ordinary Differential Equations¶

Let’s remind ourselves of the solution to first order scalar ordinary differential equations (ODEs), which take the form

\begin{align*} \frac{du}{dt} = au, \end{align*}

(1)

where $a\in \mathbb R$ is a known constant, and $u(t)$ is an unknown scalar function.

The general solution to (1) is an exponential function

\begin{align*} u(t) = ce^{at}, \tag{SOL} \end{align*}

(3)

where the constant $c\in\mathbb R$ is uniquely determined by the initial condition $u(t_0) = b$ (note we’ll often take $t_0 = 0$ to keep things simple). Substituting $t= t_0$ into (SOL), we see that

\begin{align*} u(t_0) = ce^{at_0} = b \end{align*}

(4)

so that $c = be^{-at_0}$ , allowing us to conclude that

\begin{align*} u(t) = be^{a(t - t_0)} \end{align*}

(5)

solves (1).

Example 1 (Half-life of an isotope)

The radioactivity decay of uranium-238 is governed by the differential equation

\begin{align*} \frac{du}{dt} = -\gamma u \end{align*}

(6)

where $c = u(0)$ is the initial amount of U238 at $t_0 = 0$ . We see that the amount $u(t)$ is decaying to zero exponentially quickly with “rate” γ.

An isotope’s half-life $t_*$ is how long it takes for the amount of a sample to decay to half its initial value, i.e., $u(t_*) = \frac 1 2 u(0)$ . To determine $t_*$ , we solve

\begin{align*} &u(t_*) = u(0) e^{-\gamma t_*} = \frac 1 2 u(0)\\ &\iff e^{-\gamma t_*} = \frac 1 2 \iff t_* = \frac{\log 2}{\gamma} \end{align*}

(7)

Before proceeding to the general case, we make some simple but useful observations:

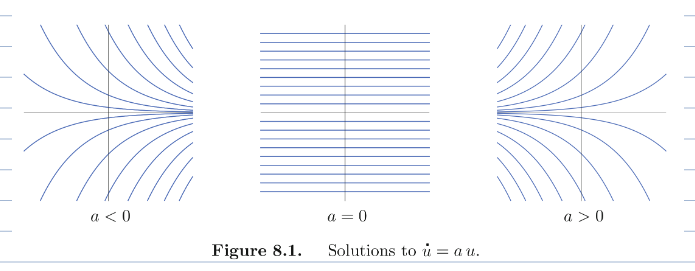
The zero function $u(t) = 0$ for all $t$ is a solution with $c=0$ . This is known as an equilibrium of fixed point solution.
If $a > 0$ , then solutions grow exponentially: this implies $u = 0$ is an unstable equilibrium, beacuse any small nonzero initial condition $u(t_0) = \epsilon$ will “blow up” far away from $u=0$ .
If $a < 0$ , the solutions decay exponentially; this implies $u = 0$ is a stable equilibrium (in fact globally asymptotically so), which means that $u(t) \to 0$ as $t\to \infty$ for any initial condition $u(t_0)$ .
The borderline case is $a = 0$ , in which case all solutions are constant, i.e., $u(t) = u(t_0)$ for all $t$ . Such systems are called marginally stable (or just stable) because while they don’t blow up on you, they also don’t converge to $u = 0$ .

3.2First Order Dynamical Systems¶

We will concerntrate most of our attention on homogenous linear time-invariant first order dynamical systems.

Definition 1 (Homogeneous linear time-invariant first order dynamical system)

For homogeneous linear time-invariant first order dynamical systems, we have a vector-valued solution

\begin{align*} \vv{u}(t) = \bm u_1(t)\\u_2(t) \\ \vdots \\ u_n(t) \em \end{align*}

(8)

which parameterizes a curve in $\mathbb{R}^n$ . This solution $\vv{u}(t)$ is assumed to obey a differential equation of the form

\begin{align*} \frac{du_1}{d_t} &= a_{11}u_1 + a_{12}u_2 + \dots + a_{1n}u_n\\ \frac{du_2}{d_t} &= a_{21}u_1 + a_{22}u_2 + \dots + a_{2n}u_n\\ &\dots\\ \frac{du_n}{d_t} &= a_{n1}u_1 + a_{n2}u_2 + \dots + a_{nn}u_n\\ \end{align*}

(9)

or more compactly,

\begin{align*} \frac{d\vv u}{dt} = A\vv u\tag{LTI} \end{align*}

(10)

for $A\in \mathbb{R}^{n\times n}$ a known constant matrix.

The question now becomes: what are the solutions to (LTI)? Well, let’s take inspiration from the scalar solution (SOL) and investigate if and when

\begin{align*} \vv u(t) = e^{\lambda t} \vv v \tag{GUESS} \end{align*}

(11)

is a solution to (LTI). Here, $\lambda \in \mathbb R$ is a constant, as is $\vv v\in \mathbb{R}^n$ . In other words, the components $u_i(t) = e^{\lambda t} v_i$ of (GUESS) are constant multiples of the same exponential function.

Let’s start by computing the time derivatives of both sides of (GUESS):

\begin{align*} \vv u(t) = e^{\lambda t} \vv v \quad\text{for all $t$} &\iff \frac{d}{dt} \vv u(t) = \frac{d}{dt} e^{\lambda t} \vv v \quad\text{for all $t$} \\ &\iff A\vv u = \lambda e^{\lambda t} \vv v \quad\text{for all $t$} \qquad\text{(by (LTI))}\\ &\iff Ae^{\lambda t} \vv v = \lambda e^{\lambda t} \vv v \quad\text{for all $t$} \qquad\text{(by (GUESS))}\\ &\iff A \vv v = \lambda \vv v \quad\text{for all $t$} \qquad\text{(since $e^{\lambda t}$ is a positive scalar)} \end{align*}

(12)

Therefore (GUESS) solves (LTI) if and only if $\lambda \vv v = A \vv v$ . Note that this is precisely the definition of an eigenvalue/eigenvector pair, which we’ve studied extensively in the previous few pages! For the rest of this page, we’ll look at how the facts we’ve learend about eigenvalues and eigenvectors play a role in the solution to linear ODEs.

4Eigenvalues and Eigenvectors in Linear ODEs¶

A key obesrvation is that we can reduce solving (LTI) to solving $n$ independent scalar ODEs when the matrix $A$ is diagonalizable. Let $V = \bm \vv{v_1} & \vv{v_2} & \dots & \vv{v_n}\em$ be the $n\times n$ matrix of the eigenvectors of $A$ , and $D = \text{diag}(\lambda_1, \dots, \lambda_n)$ , the diagonal matrix of corresponding eigenvalues. Then $A = VDV^{-1}$ so that

\begin{align*} \frac{d}{dt} \vv u = VDV^{-1} \vv u \tag{S1} \end{align*}

(13)

Rewriting this linear transformation in the eigenbasis given by $V$ , we set $V \vv y = \vv u$ so that $\vv y = V^{-1}\vv u$ and $\frac{d \vv u}{dt} = V\frac{d\vv y}{dt}$ to rewrite (S1) as

\begin{align*} V \frac{d\vv y}{d t} = VD\vv y\tag{S2} \end{align*}

(14)

Since $V$ is nonsingular, (S2) is true if and only if

\begin{align*} \frac{d\vv y}{dt} = D\vv y \tag{S3} \end{align*}

(15)

Thus by working in the coordinate system defined by the eigenbasis $V$ , we’ve reduced solving (LTI) to solving the $n$ decoupled scalar ODEs in (S3):

\begin{align*} \frac{d y_i}{dt} = \lambda_i y_i \tag{Si} \end{align*}

(16)

The general solution to (Si) is $y_i(t) = c_ie^{\lambda_i(t - t_0)}$ , with $c_i = y_i(c_0)$ . Here, $y_i(t_0)$ can be computed via $\vv y (t_0) = V^{-1} \vv u (t_0)$ .

Now, given the solution $\vv y(t) = (y_1(t), \dots, y_n(t))$ in the eigenbasis $V$ , we need to map it back to our original coordinates via

\begin{align*} \vv u(t) &= V \vv y(t) \\ &= c_1 e^{\lambda_1 (t - t_0)} \vv{v_1} + c_2 e^{\lambda_2 (t - t_0)} \vv{v_2} + \dots + c_ne^{\lambda_n (t - t_0)} \vv{v_n} \tag{SOL} \end{align*}

(17)

where we remember that $\vv c = V^{-1} u(t_0)$ .

4.1Solving Linear ODEs when $A$ is Diagonalizable¶

In the previous section, we just showed something incredibly powerful, which we summarize in the following theorem.

Theorem 1 (The solution to a homogeneous linear time-invariant first order dynamical system with diagonalizable

A

)

Let $\frac{d}{dt}\vv u = A\vv u$ define a linear ODE such that the coefficient matrix $A$ is diagonalizable. Let $\lambda_1, \lambda_2, \dots, \lambda_n$ be the eigenvalues of $A$ (counting multiplicities), and let $\vv{v_1}, \vv{v_2}, \dots, \vv{v_n}$ be the corresponding eigenvectors.

Then, any solution to this linear ODE is a linear combination of the functions

\begin{align*} \{ e^{\lambda_1 (t - t_0)}\vv{v_1}, e^{\lambda_2 (t - t_0)}\vv{v_2}, \dots , e^{\lambda_n(t - t_0)}\vv{v_n} \} \end{align*}

(18)

i.e., these form a basis for the solutions of (LTI); which particular solution we select is specified by the initial conditions via $\vv{c} = V^{-1}u(t_0)$ .

Example 2 (Solving a linear ODE with

2\times 2

coefficient matrix)

Consider $\frac{d}{dt}\vv u = A\vv u$ , with $A = \bm 1&-1\\2&4\em$ . We are given that $A$ has eigenvalue/eigenvector pairs:

\begin{align*} \lambda_1 = 2, \vv{v_1} = \bm 1\\ -1\em \quad\text{and} \quad \lambda_2 = 3, \vv{v_2} = \bm 1\\-2\em, \end{align*}

(19)

and therefore solutions $\vv u(t)$ take the form

\begin{align*} \vv u(t) = c_1 e^{\lambda_1 (t - t_0)} \vv{v_1} + c_2 e^{\lambda_2 (t - t_0)}\vv{v_2} = c_1e^{2(t - t_0)}\bm 1\\-1\em + c_2 e^{3(t - t_0)}\bm 1\\-2\em. \end{align*}

(20)

Suppose we have the requirement that $\vv u(t_0) = \bm 3\\4\em$ , then we solve

\begin{align*} \vv u(t_0) = c_1 \bm 1\\-1\em + c_2 \bm 1\\-2\em = \bm 1&1\\-1-2\em \bm c_1\\c_2\em = \bm 3\\4 \em \end{align*}

(21)

for $\bm c_1\\c_2\em = \bm 10 \\-7\em$ , and obtain the specific solution

\begin{align*} \vv u(t) = 10e^{2(t - t_0)}\bm 1\\-1\em - 7e^{3(t - t_0)}\bm 1\\-2\em. \end{align*}

(22)