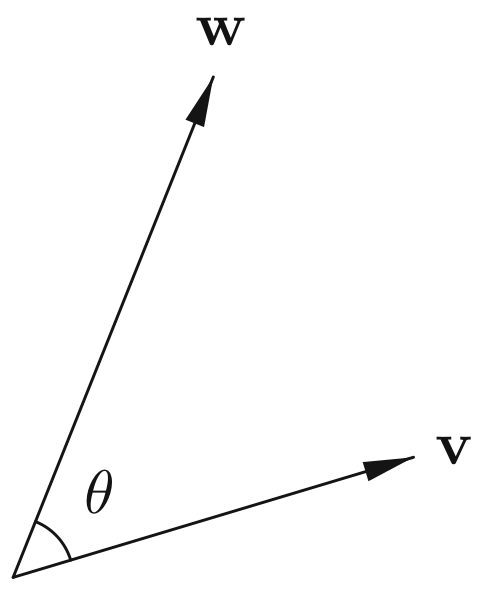
3.2 Angles, the Cauchy–Schwarz Inequality, and General Norms

1Reading¶

Material related to this page, as well as additional exercises, can be found in ALA Ch. 3.2.

2Learning Objectives¶

By the end of this page, you should know:

the Cauchy-Schwarz Inequality
the generalized angle between vectors
orthogonality between vectors
the triangle inequality
definition and examples of norms

3Generalized Angle¶

Our starting point in defining the notion of angle in a general inner product space is the familiar formula

\vv v \cdot \vv w = \|\vv v\| \|\vv w\| \cos(\theta),

(1)

where θ measures the angle between $\vv v$ and $\vv w$ .

Since $\|\cos(\theta)\| \leq 1$ , we can bound the magnitude of $\vv v \cdot \vv w$ as

|\vv v \cdot \vv w| \leq \|\vv v\|\|\vv w\|.

(2)

Definition 1 makes sense because, by (3), we know that

-1 \leq \frac{\langle \vv v, \vv w \rangle}{\|\vv v\|\|\vv w\|} \leq 1.

(5)

Hence, θ is well defined, and unique if restricted to be in $[0, \pi]$ .

4Angles between Generic Vectors¶

Example 1

The vectors $\vv v = \bm 1 \\ 0 \\ 1\em$ and $\vv w = \bm 0 \\ 1 \\ 1\em$ have dot product $\vv v . \vv w = 1$ and norms $\|\vv v\| = \|\vv w\| = \sqrt{2}$ . Hence,

\cos(\theta) = \frac{1}{\sqrt{2}\sqrt{2}} = \frac{1}{2} \Rightarrow \theta = \arccos\left(\frac{1}{2}\right) = \frac{\pi}{3} \ \textrm{rad},

(6)

which is the usual notion of angle.

We can also compute the angle between $\vv v$ and $\vv w$ with respect to the weighted inner product $\langle \vv v, \vv w \rangle = v_1w_1 + 2v_2w_2 + 3v_3w_3$ . For this inner product, $\langle \vv v, \vv w \rangle = 3, \| \vv v\| = 2, \|\vv w\| = \sqrt{5}$ . Hence,

\cos(\theta) = \frac{3}{2\sqrt{5}} = 0.67082 \Rightarrow \theta = \arccos\left(0.67082\right) = 0.83548 \ \textrm{rad}.

(7)

Example 2

We can also define angles between vectors in a generic vector space, for example, polynomials. For ${p(x) = a_0 + a_1 x +a_2x^2, q(x) = b_0 + b_1x + b_2x^2 \in P^{(2)}}$ , we define the $\langle p, q\rangle = a_0b_0 + a_1b_1 + a_2b_2$ . This agrees with the standard dot product applied to $\vv p = \bm a_0 \\ a_1 \\ a_2\em, \vv q = \bm b_0 \\ b_1 \\ b_2\em$ and hence immediately satisfies this definition. The angle between $p(x)$ and $q(x)$ is computed as

\cos(\theta) = \frac{\langle p, q \rangle}{\|p\| \|q\|} = \frac{\langle \vv p, \vv q \rangle}{\|\vv p\| \|\vv q\|}.

(8)

For example, if $p(x) = 1 + x^2$ and $q(x) = x + x^2$ , then $\langle p, q \rangle = 1$ and $\| p \| = \| q \| = \sqrt{2}$ , and ${\cos(\theta) = \frac{1}{2} \Rightarrow \theta = \frac{\pi}{3}}$ .

Python break!¶

We show how to use NumPy functions (np.dot, np.linalg.norm, np.arcos) to compute the angle between vectors. We also show how to compute cosine similarity from the cosine distance between vectors using scipy.spatial library.

# angle between vectors
import numpy as np
import scipy

v = np.array([1, 0, 1])
w = np.array([0, 1, 1])

cos_theta = np.dot(v, w)/(np.linalg.norm(v)*np.linalg.norm(w))
theta = np.arccos(cos_theta)
print("Angle between v and w is: ", theta, " rad")

# cosine distance -> cosine similarity
from scipy.spatial import distance

cosine_dist = distance.cosine(v, w)
cosine_sim = 1 - cosine_dist
print("Cosine similarity between v and w is: ", cosine_sim)

Angle between v and w is:  1.0471975511965979  rad
Cosine similarity between v and w is:  0.5

5Orthogonal Vectors¶

The notion of perpendicular vectors is an important one in Euclidean geometry. These are vectors that meet at a right angle, i.e., $\theta = \frac{\pi}{2}$ or $\theta = -\frac{\pi}{2}$ , with $\cos \theta = 0$ . This tells us that vectors $\vv v$ and $\vv w$ are perpendicular if and only if their dot product vanishes: $\vv v \cdot \vv w = 0$ (can you see why via Cauchy-Schwarz?).

We continue with our strategy of extending familiar geometric concepts in Euclidean space to general inner product spaces. For historic reasons, we use the term orthogonal instead of perpendicular.

Orthogonality is an incredibly useful and practical idea that appears all over the place in engineering, AI, and economics, which we will explore in detail next lecture.

Example 4

The polynomials $f(x) = x$ and $g(x) = 1 + x^2$ are orthogonal with respect to the inner product on $P^{(2)}$ defined previously as $\langle p, q\rangle = a_0b_0 + a_1b_1 + a_2b_2$ . Here, $a_0 = 0, a_1 = 1, a_2 = 0$ and $b_0 = 1, b_1 = 0, b_2 = 1$ . So, $\langle f, g\rangle = 0\cdot 1 + 1 \cdot 0 + 0 \cdot 1 = 0$ .

However, $f$ and $g$ are not orthogonal with respect to the inner product $\langle p, q \rangle = \int_0^1 p(x)q(x) dx$ defined on $C^{0}[0, 1]$ :

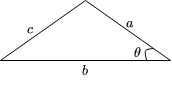
\langle f, g \rangle = \int_0^1 x(1 + x^2) dx = \int_0^1 (x + x^3) dx = \frac{x^2}{2} + \frac{x^4}{4} \bigg|_{0}^1 = \frac{1}{2} + \frac{1}{4} = \frac{3}{4} \neq 0.

(10)

6The Triangle Inequality¶

We know, e.g., from the law of cosines, that the length of one side of a triangle is at most the sum of the length of the other two sides.

\begin{align*} c^2 &= a^2 + b^2 - 2ab\cos(\theta) \\ &\leq a^2 + b^2 + 2ab \ (\textrm{since} \ \cos(\theta) \leq 1) \\ &= (a+b)^2 \\ \Rightarrow c &\leq a+b \end{align*}

(11)

The idea in (11) extends directly to the setting where we want to relate the length $\|\vv v + \vv w\|$ of the sum of vectors $\vv v$ , $\vv w$ to the lengths $\|\vv v\|$ and $\| \vv w\|$ .

Theorem 2 (Triangle Inequality)

The norm associated with an inner product satisfies the triangle inequality:

\|\vv v + \vv w\| \leq \|\vv v\| + \|\vv w\| \ \textrm{for all} \ \vv v, \vv w \in V.

(12)

Equality holds in (12) if and only if $\vv v = c \vv w$ for some positive constant $c > 0$ .

Proof 1 (Proof of Theorem 2)

This is almost exactly the same as the law of cosines. We set up a triangle as follows

and use that

\begin{align*} \|\vv v + \vv w\|^2 &= \langle \vv v + \vv w, \vv v + \vv w\rangle \\ &= \|\vv v\|^2 + 2 \langle \vv v, \vv w\rangle + \|\vv w\|^2 \\ &= \|\vv v\|^2 + 2 \|\vv v\| \|\vv w\| \cos(\theta) + \|\vv w\|^2 \\ &\leq \|\vv v\|^2 +2 \|\vv v\| \|\vv w\| + \|\vv w\|^2 \ (\textrm{Cauchy-Schwartz}) \\ &= \left(\|\vv v\| + \| \vv w\|\right)^2 \end{align*}

(13)

7Norms¶

We have seen that inner products allow us to define a natural notion of length. However, there are other sensible ways of measuring the size of a vector that do not arise from an inner product. For example suppose we choose to measure the size of a vector by its ``taxicab distance’’ where we pretend we are a cab driver in Manhattan, and we can only drive go north-south and east-west. We then end up with a different measure of length that makes lots of sense!

To define a general norm on a vector space, we will extract properties that ``make sense’’ as a measure of distance but that do not directly rely on an inner product structure (like angles).

7.1Describing Definition 3¶

Axiom (i) says ``length’’ should always be non-negative, and only the zero vector has zero length (seems reasonable!)

Axiom (ii) says if I stretch/shrink a vector $\vv v$ by a factor $c \in \mathbb{R}$ , then the length should scale accordingly (this is why we call $c \in \mathbb{R}$ a scalar!). Note that $c<0$ means we stretch/shrink and flip $\mathbf{v}$ , but flipping shouldn’t affect length, so $\|c\vv v\| = \|-c\vv v\| = |c|\|\mathbf{v}\|$ .

Axiom (iii) tells us that lengths of sums of vectors should ``behave as if there is a cosine rule’’ even if there is no notion of angle. This is a less intuitive property but has been identified as a key property to make norms useful to work with.

We will introduce two other commonly used norms in practice, but you should know that there are many many more.

Common norms

The 1-norm of a vector $\vv v = \bm v_1 \\ v_2 \\ \vdots \\ v_n\em \in \mathbb{R}^n$ is the sum of the absolute values of its entries:
$\|\vv v\|_1 = |v_1| + |v_2| + \ldots + |v_n|$
(17)
which we recognize as our taxi cab distance.
The $\infty-$ norm or max-norm is given by the maximal entry in absolute value:
$\|\vv v\|_{\infty} = \max\{|v_1|, |v_2|, \ldots, |v_n|\}.$
(18)

Checking the axioms of Definition 3 is a good exercise for you. The basic inequality $|a + b| \leq |a| + |b|$ for $a, b \in \mathbb{R}$ is all you need.

The 1-norm, $\infty-$ norm and Eucledian norm (also called the 2-norm) are examples of the general $p-$ norm:

\|\vv v\|_p = \left(\sum_{i=1}^n|v_i|^p\right)^{\frac{1}{p}} \ (\textrm{p-norm})

(19)

which can be shown to be a valid norm for $1 \leq p < \infty$ (the $\infty-$ norm is a limiting case of $p-$ norm as $p \to \infty$ ).

The hard part in showing $p-$ norm is a norm is verifying the triangle inequality (axiom 3), which is also known as Minkowski’s inequality.

# Different norms

v = np.array([1, -2])
v1 = np.linalg.norm(v, ord=1)
v2 = np.linalg.norm(v)
vinf = np.linalg.norm(v, ord=np.inf)
print("\n1-norm: ", v1, "\n2-norm: ", v2, "\ninfinity norm: ", vinf)


1-norm:  3.0 
2-norm:  2.23606797749979 
infinity norm:  2.0